Question

An acetate buffer solution is prepared by combining 50 ml of .20 M acetic acid and 50 ml of .20 M sodium acetate. A 5 ml sample of .10 M naoh is added to the buffer solution. what is the final pH of the solution? pKa of acetic acid is 4.7

Answer 1

`\large \boxed{4.7}`

Step-by-step explanation:

The equation for the buffer equilibrium is

HA + H₂O ⇌ H₃O⁺ + A⁻

1. Calculate the composition of the original buffer

`\text{ Initial moles of HA} = \text{50 mL} * \frac{\text{0.20 mmol }}{\text{1 mL}} = \text{10 mmol}\\\\\text{ Initial moles of A}^(-) = \text{50 mL} * \frac{\text{0.20 mol }}{\text{1.00 L}} = \text{10 mmol}`

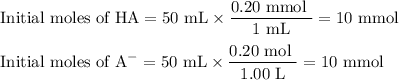
So you have 10 mmol of HA and 10 mmol of A⁻ in 100 mL of the buffer.

2. pH after adding NaOH

(a) Find new composition of the buffer

The base reacts with the HA and forms A⁻

`\text{Moles of OH$^(-)$ added} = \text{5 mL } * \frac{\text{0.10 mmol}}{\text{ 1 mL}} = \text{0.50 mmol}`

HA + H₂O ⇌ H₃O⁺ + A⁻

I/mmol: 10 10

C/mmol: -0.5 +0.5

E/mmol: 9.5 10.5

(b) Find the new pH

`\begin{array}{rcl}\text{pH} & = & \text{pK}_{\text{a}} + \log \left(\frac{[\text{A}^(-)]}{\text{[HA]}}\right )\\\\& = & 4.7 +\log \left((10.5)/(9.5)\right )\\\\& = & 4.7 + \log1.11 \\& = & 4.7 +0.043\\& = & \mathbf{4.7}\\\end{array}\\\text{The new pH is $\large \boxed{\textbf{4.7}}$}`