Answer:
Option A - neither even nor odd
Explanation:
Given :
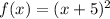
To find : Determine whether the function below is an even function, an odd function, both, or neither ?
Solution :
We know that,
1) If f(-x)=f(x) it is an even function.
2) If f(-x)=-f(x) it is a odd function.
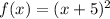
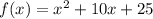
Substitute x with -x in the function,
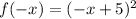
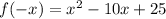
The function does not comply with the definitions.
The function is neither even nor odd.
Therefore, option A is correct.