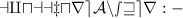
To solve this problem, let's denote the width of the rectangle as $w$ (in cm).
According to the given information, the length of the rectangle is 6 cm more than the width, so the length can be represented as $w + 6$ (in cm).
The perimeter of a rectangle is given by the formula:
$$\text{{Perimeter}} = 2(\text{{length}} + \text{{width}})$$
Substituting the values, we have:
$64 = 2((w + 6) + w)$
Now, let's solve for $(w)$:
$64 = 2(2w + 6)$
$64 = 4w + 12$
$4w = 64 - 12$
$4w = 52$
Dividing both sides of the equation by 4, we get:
$w = \frac{{52}}{{4}}$
$w = 13$
So, the width of the rectangle is 13 cm.
Substituting the value of $w$ back into the expression for the length:
$$\text{{Length}} = w + 6 = 13 + 6 = 19$$
Therefore, the dimensions of the rectangle are 13 cm (width) and 19 cm (length).