Answer:
The equation which represent the area of forest creases each year is 2000 km²
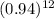 and
and
The area is 952 km² .
Explanation:
Given as :
The rate of depreciation of forest area each year = r = 6%
The initial area of forest = i = 2000 square kilometers
Let The final area of forest = f = x square kilometers
The time period for depreciation = 12 year
Now, According to question
The final area of forest = The initial area of forest ×
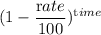
Or, f = i ×

Or, f = 2000 km² ×
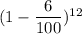
Or, f = 2000 km² ×
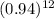
∴ f = 2000 km² × 0.475920
I.e f = 951.84 ≈ 952 km²
So, The equation which represent the area of forest creases each year = f = 952 km²
Hence,The equation which represent the area of forest creases each year is 2000 km²
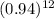 and the area is 952 km² . Answer
and the area is 952 km² . Answer