Answer:
0.5 m
14.00595
8 m/s, 0.0625 s
5.71314 m/s
Step-by-step explanation:
k = Spring constant = 128 N/m
A = Amplitude
E = Energy in spring = 16 J
Energy in spring is given by
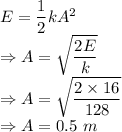
The amplitude is 0.5 m
Time period is given by
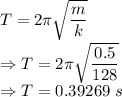
Number of oscillations is given by
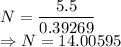
The number of oscillations is 14.00595
For maximum speed
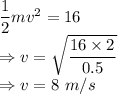
The maximum speed is 8 m/s
For a distance of 0.5 m which is the amplitude
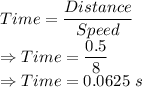
The time taken would be 0.0625 s
The maximum kinetic energy is equal to the mechanical energy
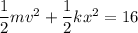
At x = 0.35 m
The speed of the block is 5.71314 m/s