Question

A cylindrical blood vessel is partially blocked by the buildup of plaque. At one point, the plaque decreases the diameter of the vessel by 67.0 %. The blood approaching the blocked portion has speed v 0 . Just as the blood enters the blocked portion of the vessel, what is its speed v , expressed as a multiple of v 0 ?

Answer 1

speed of flow of blood in the blocked portion of the vessel is 9.18 vo

Step-by-step explanation:

given data

diameter of the vessel = 67.0 %

to find out

what is its speed v expressed as a multiple of vo

solution

we know here that Plaque decreases diameter of the vessel by 67%

s here diameter in the blocked portion = 33% of diameter in unblocked portion so

we will apply here Continuity equation that is express as

Ao×Vo = A1×V1 ...................1

here Ao is Cross-sectional area of the cylindrical blood vessel that is =
`(\pi do^2)/(4)`

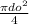
and do is Diameter of the cylindrical blood vessel and vo is Speed of flow of blood in the blood vessel

and d1 is diameter of the vessel in the blocked portion of the vessel that is = 0.33 do and A1 is cross section area of the vessel in the blocked portion that is =
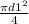`(\pi d1^2)/(4)` and v1 is Speed of flow of blood in the blocked portion of the vessel

so now we put value in equation 1 we get

Ao×Vo = A1×V1

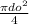`(\pi do^2)/(4)` × vo =
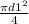`(\pi d1^2)/(4)` × v1

do²×vo = d1²×v1

do²×vo = d1²×v1

do²×vo = (0.33 do)²×v1

solve it we get

v1 = 9.18 vo

so speed of flow of blood in the blocked portion of the vessel is 9.18 vo