Question

Please need help on these two cause I’m very lost on them

Answer 1

see explanation

Explanation:

Given

f(x) = (x - 4)(2x - 1)²(x - 2)²

To find the roots equate f(x) to zero, that is

(x - 4)(2x- 1)²(x - 2)² = 0

Equate each of the factors to zero and solve for x

x - 4 = 0 ⇒ x = 4

2x - 1 = 0 ⇒ x =
`(1)/(2)` ← with multiplicity 2

x - 2 = 0 ⇒ x = 2 ← with multiplicity 2

Hence the roots are

{ 4,
`(1)/(2)`, 2 }

Given

f(x) = x³ + 4x² + 7x + 6

Note that

f(- 2) = (- 2)³ + 4(- 2)² + 7(- 2) + 6 = - 8 + 16 - 14 + 6 = 0

Since f(- 2) = 0 then by the factor theorem x = - 2 is a root and (x + 2) a factor

Using synthetic division

- 2 | 1 4 7 6

- 2 - 4 - 6

--------------

1 2 3 0

Thus

f(x) = (x + 2)(x² + 2x + 3)

Solve x² + 2x + 3 using the quadratic formula

with a = 1, b = 2 and c = 3

x = (- 2 ±
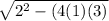`√(2^2-(4(1)(3))` ) / 2

= ( - 2 ±
`√(4-12)` ) / 2

= ( - 2 ±
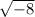`√(-8)` ) / 2

= (- 2 ± 2i
`√(2)` ) / 2

= - 1 ± i
`√(2)`

Hence roots are

{ - 2, - 1 + i
`√(2)`, - 1 - i
`√(2)` }