Question

A 1850 kg car traveling at 13.8 m/s collides with a 3100 kg car that is initally at rest at a stoplight. The cars stick together and move 1.91 m before friction causes them to stop. Determine the coefficient of kinetic friction between the cars and the road, assuming that the negative acceleration is constant and all wheels on both cars lock at the time of impact.

Answer 1

To solve this problem, it is necessary to apply the concepts related to the conservation of momentum, the kinematic equations for the description of linear motion and the definition of friction force since Newton's second law.

The conservation of momentum can be expressed mathematically as

`m_1v_1+m_2v_2 = (m_1+m_2)v_f`

Where,

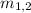`m_(1,2)`= Mass of each object

`v_(1,2)` = Initial Velocity of each object

`v_f`= Final velocity

Replacing we have that,

`m_1v_1+m_2v_2 = (m_1+m_2)v_f`

`1850*13.8+3100*0 = (1850+3100)v_f`

`v_f = 5.1575m/s`

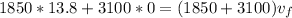
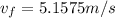
With the final speed obtained we can determine the acceleration through the linear motion kinematic equations, that is to say

`v_f^2-v_i^2 = 2ax`

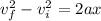
Since there is no initial speed, then

`v_f^2 = 2ax`

`5.1575^2 = 2a (1.91)`

`a = 6.9633m/s^2`

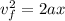
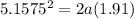
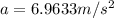
Finally with the acceleration found it is possible to find the friction force from the balance of Forces, like this:

`F_f = F_a \\\mu N = m*a \\\mu = (ma)/(N)\\\mu = (ma)/(mg)\\\mu = (a)/(g)\\\mu = (6.9633)/(9.8)\\\mu = 0.7105`

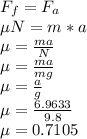
Therefore the Kinetic friction coefficient is 0.7105