Question

At most, how many bright fringes can be formed on each side of the central bright fringe (not counting the central bright fringe) when light of 625 nm falls on a double slit whose spacing is 2.95×10-6 m? At most, how many bright fringes can be formed on each side of the central bright fringe (not counting the central bright fringe) when light of 625 nm falls on a double slit whose spacing is 2.95×10-6 m? A. 2 B. 3 C 4 D. 5 E. 6

Answer 1

B

Step-by-step explanation:

Answer 2

To solve this problem it is necessary to apply the concepts related to the principle of overlap and constructive interference.

By definition we know that

`dsin\theta = n\lambda`

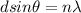
Where,

d = Distance between slits

n = Number of fringes (or number of repetition of the spectrum)

`\lambda` = Wavelength

Our values are given as

`d = 6.95*10^(-6)m`

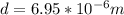
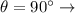`\theta = 90\° \rightarrow` The angle is 90 degrees because the angle is the furthest angle the light can rotate from out of the slits.

`\lambda = 625*10^(-9)m`

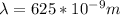
Replacing we have that

dsin\theta = n\lambda

`(2.95*10^(-6))sin(90) = n(625*10^(-9))`

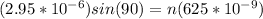
n = \frac{(2.95*10^{-6})}{(625*10^{-9})}

n = 4.72

Therefore 4 complete bright fringes are formed and the number of bright fringes without including the central bright fringe is 3. The correct answer is B.