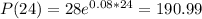Answer:
a) P(24) = 1025.
b) P(24) = 191.
Explanation:
This population can be modeled by the following exponential model.

In which P(t) is the population after t hours,
 is the initial population and r is the decimal growth rate.
is the initial population and r is the decimal growth rate.
The initial number of bacteria in the culture is 28. This means that
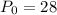 .
.
Population after 24 hours.
(a) No antibiotic is present, so the relative growth rate is 15%.
So r = 0.15.

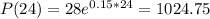
(b) An antibiotic is present in the culture, so the relative growth rate is reduced to 8%.
So r = 0.08.