The system of equations could be used to determine the number of each type of ticket sold is:
s + p + t = 490
8s + 10p + 12t = 4600
s + p = 6t
Number of each type of ticket sold is:
number of student tickets sold = 220
number of pre-sale non student ticket sold = 200
number of ticket sold at door = 70
Solution:
Let "s" be the number of student tickets sold
Let "p" be the number of pre-sale non student ticket sold
Let "t" be the number of ticket sold at door
Cost of 1 student ticket = $ 8
Cost of 1 pre-sale non student ticket = $ 10
Cost of 1 ticket sold at door = $ 12
From given information,
490 tickets were sold. So we can frame a equation as:
number of student tickets sold + number of pre-sale non student ticket sold + number of ticket sold at door = 490
s + p + t = 490 ---------- eqn 1
Also given that, The total income from ticket sales was $4600
So we can frame a equation as:
number of student tickets sold x Cost of 1 student ticket + number of pre-sale non student ticket sold x Cost of 1 pre-sale non student ticket + number of ticket sold at door x Cost of 1 ticket sold at door = $ 4600
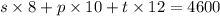
8s + 10p + 12t = 4600 ------ eqn 2
The combined number of student and pre-sale tickets was 6 times more than the tickets sold at the door
s + p = 6t --------- eqn 3
So eqn 1 eqn 2 and eqn 3 could be used to determine the number of each type of ticket sold
Let us solve eqn 1, eqn 2, eqn 3 to find values of "s" "p" and "t"
Substitute eqn 3 in eqn 1
6t + t = 490
7t = 490
t = 70
Substitute t = 70 in eqn 2
8s + 10p + 12(70) = 4600
8s + 10p = 3760 ----- eqn 4
Substitute t = 70 in eqn 3
s + p = 6(70)
s + p = 420 ----- eqn 5
Multiply eqn 5 by 8
8s + 8p = 3360 ----- eqn 6
Subtract eqn 6 from eqn 4
8s + 10p = 3760
8s + 8p = 3360
(-) ---------------------
2p = 400
p = 200
Substitute p = 200 in eqn 5
s + 200 = 420
s = 220
Summarizing the results:
number of student tickets sold = 220
number of pre-sale non student ticket sold = 200
number of ticket sold at door = 70