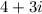Question

Please help me!!!! with both​

Answer 1

Part 11)
`a_n=a_(n-1)-16`,
`a_1=17`

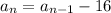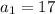
Part 2) 4+3i

Explanation:

Part 11) write a recursive rule for the sequence

`17,1,-15,-31,...`

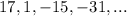
Let

`a_1=17\\a_2=1\\a_3=-15\\a_4=-31`

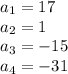
we know that

`a_2-a_1=1-17=-16` ---->
`a_2=a_1-16`

`a_3-a_2=-15-1=-16` ---->
`a_3=a_2-16`

`a_4-a_3=-31-15=-16` ---->
`a_4=a_3-16`

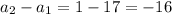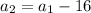
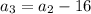
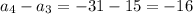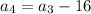
This is an arithmetic sequence

In an Arithmetic Sequence the difference between one term and the next is a constant, and this constant is called the common difference (d).

In this problem the common difference is equal to
`d=-16`

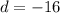
therefore

A recursive rule for the sequence is

`a_n=a_(n-1)+d`

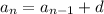
substitute the value of d

`a_n=a_(n-1)-16`

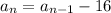
where

`a_1=17`

Part 12) What is the complex conjugate of 4-3i?

we know that

The complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign

so

we have that

the real part of the given number is 4 and the the imaginary part is -3i

so

the imaginary part equal in magnitude but opposite in sign is +3i

therefore

the complex conjugate of the given number is equal to

`4+3i`