Question

Thermopane window is constructed, using two layers of glass 4.0 mm thick, separated by an air space of 5.0 mm.

If the temperature difference is 20° C from the inside of the house to the outside air, what is the rate of heat flow through this window?

(Thermal conductivity for glass is 0.84 J/s⋅m⋅°C and for air 0.023 4 J/s⋅m⋅°C.)
a. 7 700 Wb. 1 900 Wc. 547 Wd. 180 W

Answer 1

To solve this problem it is necessary to apply the concepts related to rate of thermal conduction

`(Q)/(t) = (kA\Delta T)/(d)`

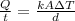
The letter Q represents the amount of heat transferred in a time t, k is the thermal conductivity constant for the material, A is the cross sectional area of the material transferring heat,
`\Delta T`, T is the difference in temperature between one side of the material and the other, and d is the thickness of the material.

The change made between glass and air would be determined by:

`((Q)/(t))_(glass) = ((Q)/(t))_(air)`

`k_(glass)((A)/(L))_(glass) \Delta T_(glass) = k_(air)(A/L)_(air) \Delta T_(air)`

`\Delta T_(air) = ((k_(glass))/(k_(air)))((L_(air))/(L_(glass))) \Delta T_(glass)`

`\Delta T_(air) = ((0.84)/(0.0234))((5)/(4)) \Delta T_(glass)`

`\Delta T_(air) = 44.9 \Delta T_(glass)`

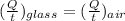
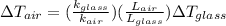
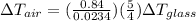
There are two layers of Glass and one layer of Air so the total temperature would be given as,

`\Delta T = \Delta T_(glass) +\Delta T_(air) +\Delta T_(glass)`

`\Delta T = 2\Delta T_(glass) +\Delta T_(air)`

`20\°C = 46.9\Delta T_(glass)`

`\Delta T_(glass) = 0.426\°C`

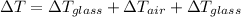
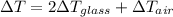
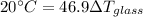
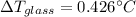
Finally the rate of heat flow through this windows is given as,

`\Delta {Q}{t} = k_(glass)(A)/(L_(glass))\Delta T_(glass)`

`\Delta {Q}{t} = 0.84*24*10 -3*0.426`

`\Delta {Q}{t} = 179W`

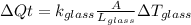
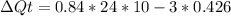
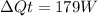
Therefore the correct answer is D. 180W.