Question

The average daily volume of a computer stock in 2011 was p = 35.1 million shares, according to a reliable source. A stock analyst believes that the stock volume in 2014 is different from the 2011 level. Based on a random sample of 40 trading days in 2014, he finds the sample mean to be 30.9 million shares, with a standard deviation of s = 11.8 million shares. Test the hypotheses by constructing a 95% confidence interval. Complete parts (a) through (c) below. A. State the hypotheses for the test. B. Construct a 95% confidence interval about the sample mean of stocks traded in 2014.​C. Determine if the researcher

Answer 1

a)Null hypothesis:
`\mu=35.1`

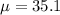
Alternative hypothesis:
`\mu \\eq 35.1`

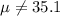
b) The 95% confidence interval would be given by (27.131;34.669)

c) Since the confidence interval contains the value of interest 35.1 we don't have enough evidence to reject the null hypothesis at 5% of significance.

Explanation:

Data given and notation

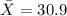`\bar X=30.9` represent the sample mean

s=11.8 represent the sample deviation

n=40 sample size

Confidence =0.95 or 95%

Part a

On this case the correct system of hypothesis would be:

Null hypothesis:
`\mu=35.1`

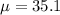
Alternative hypothesis:
`\mu \\eq 35.1`

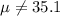
Part b

The confidence interval for the mean is given by the following formula:

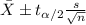`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

In order to calculate the critical value
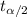`t_(\alpha/2)` we need to find first the degrees of freedom, given by:

`df=n-1=40-1=39`

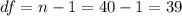
Since the Confidence is 0.95 or 95%, the value of
`\alpha=0.05` and
`\alpha/2 =0.025`, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.025,39)".And we see that
`t_(\alpha/2)=2.02`

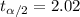
Now we have everything in order to replace into formula (1):

`30.9-2.02(11.8)/(√(40))=27.131`

`30.9-2.02(11.8)/(√(40))=34.669`

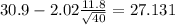
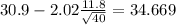
So on this case the 95% confidence interval would be given by (27.131;34.669)

Part c

​(c) Determine if the researcher will reject the null hypothesis.

Since the confidence interval contains the value of interest 35.1 we don't have enough evidence to reject the null hypothesis at 5% of significance.