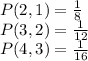Answer:
b. for X =
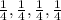
for Y=
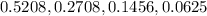
c.

Explanation:
First we assume X and Y are independent variables. For X and Y to be a joint probability mass function, the following equation must be true

Let see if this hold.From the equation, describing the probability at any giving value is
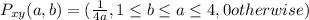
hence we can deduce the table below(see attachment)
NOTE: from the table 'b' can never be greater than 'a' when this is so, the probability is '0' these are the rows left empty in the table diagram in the attachment below.
Now we can prove the equation

that all probability from the table, when added equals '1'.
Hence that proves that this is indeed a joint probability function.
b. The Marginal probability mass function of x is written as
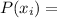 ε
ε
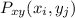
Hence at
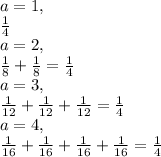
The Marginal probability mass function of Y is written as
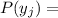 ε
ε
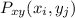
Hence at
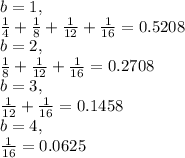
c. P (X = Y + 1), at this value, when b=1, a=2,