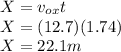Question

A baseball player standing on a platform throws a baseball out over a level playing field. The ball is released from a point 3.50 m above the field with an initial speed of 14.3 m/s at an upward angle of 27.0 degrees above the horizontal. What horizontal distance will the ball travel before hitting the ground?

Answer 1

22.1 m

Step-by-step explanation:

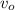`v_(o)` = initial speed of ball = 14.3 m/s

`\theta` = Angle of launch = 27°

Consider the motion of the ball along the vertical direction.

`v_(oy)` = initial speed of ball =
`v_(o) Sin\theta = 14.3 Sin27 = 6.5 ms^(-1)`

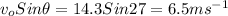
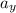`a_(y)` = acceleration due to gravity = - 9.8 ms⁻²

`t` = time of travel

`y` = vertical displacement = - 3.50 m

Using the kinematics equation that suits the above list of data, we have

`y = v_(oy) t + (0.5) a_(y) t^(2) \\- 3.50 = (6.5) t + (0.5) (- 9.8) t^(2)\\- 3.50 = (6.5) t - 4.9 t^(2)\\t = 1.74 s`

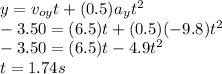
Consider the motion of the ball along the horizontal direction.

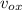`v_(ox)` = initial speed of ball =
`v_(o) Cos\theta = 14.3 Cos27 = 12.7 ms^(-1)`

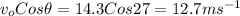
`X` = Horizontal distance traveled

`t` = time taken = 1.74 s

Since there is no acceleration along the horizontal direction, we have

`X = v_(ox) t\\X = (12.7)(1.74)\\X = 22.1 m`