Question

1.

A gym has two membership plans.
The Gold Plan costs 50 dollars per month and 3 dollars per visit.
The Platinum Plan costs 20 dollars per month and 6 dollars per visit.​

Answer 1

The number of visit so that both plan cost same is 10 .

Both the plan has equivalent choice of benefit

Explanation:

Given as :

A gym has two membership plans.

For Gold plan

The charge per month = $50

The charge per visit = $3

For Platinum plan

The charge per month = $20

The charge per visit = $6

Let The number of visit for which each plan be same = n visits

Now, According to question

∵ Each plan cost to be same

So,

The charge per month for gold plan+ The charge per visit × numbers of visit = The charge per month for platinum plan+ The charge per visit × numbers of visit

I.e $50 + $3 × n = $20 + $6 × n

Or, $50 - $20 = $6 × n - $3 × n

Or, $30 = ($6 - $3) × n

Or, $30 = $3 × n

∴ n =
`(30)/(3)`

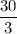
I.e n = 10

So, The number of visits = n = 10

Now, For Gold plan

The charge per month = $50

The charge per visit = $3 × 10 = $30

So, Total charge for gold plan = $50 + $30 = $80

Similarly For Platinum plan

The charge per month = $20

The charge per visit = $6×10 = $60

So, For Platinum plan ,total charge = $20 + $60 = $80

Hence, The number of visit so that both plan cost same is 10

and both the plan has equivalent benefit. Answer