Question

The degradation of CF3CH2F (an HFC) by OH radicals in the troposphere is first order in each reactant and has a rate constant of k = 1.6 x 10^8 M^-1s^-1 at 4°C.

Part A) If the tropospheric concentrations of OH and CF3CH2F are 8.1 x 10^5 and 6.3 x 10^8 molecules/cm^3, respectively, what is the rate of reaction at this temperature in M/s?

Answer 1

2.1 × 10⁻¹⁹ M/s

Step-by-step explanation:

Let's consider the degradation of CF₃CH₂F by OH radicals.

CF₃CH₂F + OH → CF₃CHF + H₂O

Considering the order of reaction for each reactant is 1 and the rate constant is 1.6 × 10⁸ M⁻¹s⁻¹, the rate law is:

r = 1.6 × 10⁸ M⁻¹s⁻¹.[CF₃CH₂F].[OH]

where,

r is the rate of the reaction

If the tropospheric concentrations of OH and CF₃CH₂F are 8.1 × 10⁵ and 6.3 × 10⁸ molecules/cm³, respectively, what is the rate of reaction at this temperature in M/s?

The Avogadro's number is 6.02 × 10²³ molecules/mole.

The molar concentration of OH is:

`(8.1 * 10^(5)molecules)/(cm^(3)).(1mol)/(6.02 * 10^(23)molecules  ).(1000cm^(3) )/(1L)  =1.3 * 10^(-15) M`

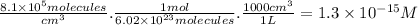
The molar concentration of CF₃CH₂F is:

`(6.3 * 10^(8)molecules)/(cm^(3)).(1mol)/(6.02 * 10^(23)molecules  ).(1000cm^(3) )/(1L)  =1.0 * 10^(-12) M`

r = 1.6 × 10⁸ M⁻¹s⁻¹ × 1.0 × 10⁻¹² M × 1.3 × 10⁻¹⁵ M = 2.1 × 10⁻¹⁹ M/s