Answer
given,
D = 50 mm = 0.05 m
d = 10 mm = 0.01 m
Force to compress the spring
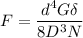
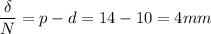
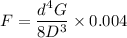
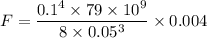
F = 3160 N
stress correction factor from stress correction curve is equal to 1.1
now, calculation of corrected stress
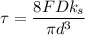
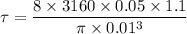
= 442.6 Mpa
The tensile strength of the steel material of ASTM A229 is equal to 1300 Mpa
now,
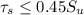
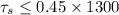
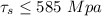
since corrected stress is less than the
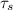
hence, spring will return to its original shape.