Question

The nuclei of the 02 molecule are separated by a dis- tance 1.20 X m. The mass of each oxygen atom in the molecule is 2.66 >< 10-26 kg.

(a) Determine the rotational energies of an oxygen molecule in electron volts for the levels corresponding to J = 0, 1, and 2.
(b) The effective force constant k between the atoms in the oxygen molecule is 1 177 N/ m. Determine the vibrational energies (in electron volts) corresponding to v = 0, 1, and 2.

Answer 1

given,

distance between the nuclei of an O₂ molecule = 1.20 x 10⁻¹⁰ m

mass of oxygen atom = 2.66 x 10⁻²⁶ Kg

the reduced mass of O₂ molecule =

`\mu=(m_1m_2)/(m_1+m_2)`

`\mu=(m_0 m_0)/(m_0+m_0)`

`\mu=(m_0)/(2)`

`\mu=(2.66 * 10^(-26))/(2)`

`\mu=1.33 * 10^(-26)`

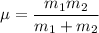
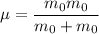
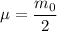
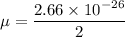
moment of inertia of O₂ molecule

`I = \mu r^2`

`I = 1.33 * 10^(-26) * (1.2* 10^(-10))^2`

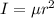
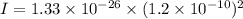
I = 1.9152 x 10⁻⁴⁶ kg.m²

a) Rotational energy of oxygen molecule

`E_j = (h^2)/(2l)j(j+1)`

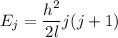
J = 0

`E_j =0`

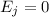
J = 1

`E_1= (h^2)/(2l)(1)(1+1)`

`E_1= (h^2)/(l)`

`E_1= ((1.055 * 10^(-34))^2)/(1.9152* 10^(-46))`

`E_1=5.81* 10^(-23)J`

`E_1=(5.81* 10^(-23)J)/(1.6* 10^(-19))`

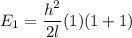
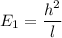
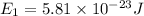
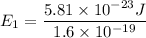
E₁ = 3.63 x 10⁻⁴ eV

J = 2

`E_2= (h^2)/(2l)(2)(2+1)`

`E_2= 3(h^2)/(l)`

`E_2= 3* 3.36 * 10^(-4)`

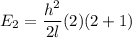
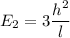
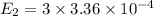
E₂ = 1.089 x 10⁻³ eV

b) Effective force constant between the molecule

`E = (v+(1)/(2))(h)/(2\pi)\sqrt{(k)/(m)}`

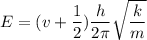
for v = 0

`E =(h)/(4\pi)\sqrt{(k)/(m)}`

`E =(1.055* 10^(-34))/(4\pi)\sqrt{(1177)/(2.66* 10^(-26))}`

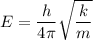
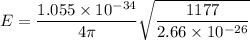
E = 1.569 x 10⁻²¹ J

`E = (1.569 * 10^(-21))/(1.6* 10^(-19))`

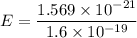
E₀ = 9.8 x 10⁻³ eV

for v = 1

E₁ = 3 E₀

E₁ = 3 x 9.8 x 10⁻³

E₁ = 29.4 x 10⁻³ eV

For v = 2

E₂ = 5 E₀

E₂ = 5 x 9.8 x 10⁻³

E₂ = 49 x 10⁻³ eV