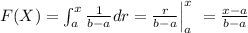Answer:
a)
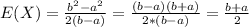
b)
![Var(X) =E(X^2) -[E(X)]^2](https://img.qammunity.org/2020/formulas/mathematics/college/qmb770lo21ypbr27fgy14e97o87wdwlmzl.png)
So first we need to find the second central moment like this:
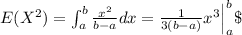

And now we can find the variance like this:
![Var(X) =(b^2+ab+a^2)/(3) -[(b+a)/(2)]^2](https://img.qammunity.org/2020/formulas/mathematics/college/wg9i5pvh7mqej2jowbeheyh2x0vywo3ir0.png)
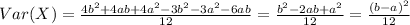
c)
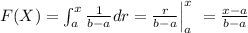
Explanation:
For this case we assume that

And the density function is given by
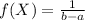
Part a
In order to find the expected value we need to do the following integral:
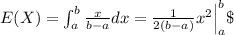
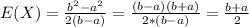
And yes agree with the intuition since is the middle value of the interval (a,b)
Part b
For this case we need to use the definition of variance:
![Var(X) =E(X^2) -[E(X)]^2](https://img.qammunity.org/2020/formulas/mathematics/college/qmb770lo21ypbr27fgy14e97o87wdwlmzl.png)
So first we need to find the second central moment like this:
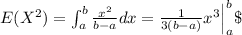

And now we can find the variance like this:
![Var(X) =(b^2+ab+a^2)/(3) -[(b+a)/(2)]^2](https://img.qammunity.org/2020/formulas/mathematics/college/wg9i5pvh7mqej2jowbeheyh2x0vywo3ir0.png)
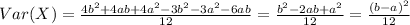
Part c
In order to find the cumulative distribution function we just ned to do the following integral: