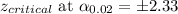Question

The lengths of my last 12 phone calls have been roughly 3, 8, 3, 5, 1, 13, 9, 2, 7, 3, 13, and 2 minutes. Long experience suggests that the standard deviation is about 5 minutes.

a) I am asked what the average length of one of my phone calls is, and I shall estimate it by ; calculate this estimate and give its standard deviation (standard error).
b) Assuming this is a large enough sample, write down a 98% confidence interval for the true value μ.

Answer 1

98% Confidence Interval: (2.387,9.113 )

Explanation:

We are given the following data set:

3, 8, 3, 5, 1, 13, 9, 2, 7, 3, 13, 2

a) Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(69)/(12) = 5.75`

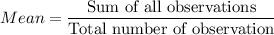
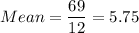
Sum of squares of differences = 196.25

`S.D = \sqrt{(196.25)/(11)} = 4.044`

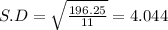
b) 98% Confidence Interval:

`\bar{x} \pm z_(critical)\displaystyle(\sigma)/(√(n))`

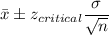
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.02) = \pm 2.33`

`5.75 \pm 2.33(\displaystyle(5)/(√(12)) ) = 5.75 \pm 3.363 = (2.387,9.113 )`