Answer:
The number of years in which house value goes up is 145 years .
Explanation:
Given as :
The initial purchased value of the house = p = $179,300,00
The value of house goes up every years at the rate = r = 4%
Let The number of years in which house value goes up = t years
The value of the house after t years = $A = $5197,230,002
Now, According to question
The value of the house after t years = The initial purchased value of the house ×
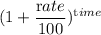
I.e A = $p ×
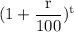
Or,$5197,230,002 = $17930000 ×
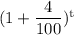
Or,
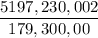 =
=
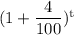
Or, 289.86 =
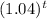
Now, taking Log both side
So,
 289.86 =
289.86 =

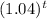
or, 2.462 = t ×
/(0.01703)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rguf2g59ywrbx2og22mzf08nspb4cgz36p.png)
I.e t = 144.56 ≈ 145
So, Number of years = t = 145 years
Hence The number of years in which house value goes up is 145 years . Answer