Question

The teacher gave this question and I'm having a hard time answering it. We're allowed to use a calculator.

Answer 1

The equation is:

`y=0.0368x^(2)+1.454b`

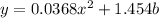
The stopping distance at 65mph will be 250ft

Why?

We can find the equation using any of the input/outputs given in the table.

The quadratic equation will be:

`ax^(2) +bx+c=y\\`

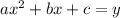
Also, remember that if the speed of the car is 0, the stopping distance will be also 0, so, the constant value "c" is not necessary in this case.

`ax^(2) +bx+=y\\`

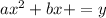
Let's use the inputs 35 and 45, and their outputs, 96 and 140.

We will have two equations with two variables, so, we can solve it:

Substituting 35 and 96:

`ax^(2) +bx+=y\\`

`a(35^(2)) +b(35)=96\\1225a+35b=96`

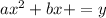
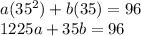
Subsituting 45 and 140:

`ax^(2)+bx+=y\\`

`a(45^(2)) +b(45)=140\\2025a+45b=140`

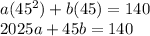
Now, we have two equations, let's solve it by elimination: Multiply the first by 9, and the second equation by 7, and then, substract the first one from the second one:

`\left \{ {{1225a+35b=96} \atop {2025a+45b=140}} \right. \\\\\left \{ {{1225a*9+35b*9=96*9} \atop {2025a*7+45b*7=140*7}} \right. \\\\\left \{ {{11025a+315b=864} \atop {14175a+315b=980}} \right. \\\\(14175a-11025a)+(315b-315b)=980-864\\\\3150a=116\\\\a=0.0368`

Now, subsitutitng "a" into the first equation to find "b" we have:

`1225*0.0368+35b=96\\\\35b=96-45.08\\\\b=(50.92)/(35)=1.454`

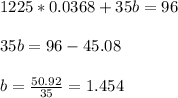
Hence, we have that the quadratic equation will be:

`y=0.0368x^(2)+1.454b`

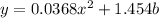
Now, predicting the stopping distance and 65mph we have:

`y=0.0368(65)^(2)+1.454*(65)=250ft`

Have a nice day!