Question

A recent study by a major financial investment company was interested in determining whether the annual percentage change in stock price for companies is linearly related with the annual percent change in profits for the company. The following data was determined for 7 randomly selected companies: Col1 % Change Stock Price (Y) 8.4 9.5 13.6 -3.2 7 18.4 -2.1Col2 % Change in Profit (X) 4.2 5.6 11.2 4.5 12.2 12 -13.4 Based upon this sample information, which of the following is the regression equation? a. y? 1.19-3.00 x b· y?=-4.198-0.612x c. y? =+4.198 x d, y? = 4.198 + 0.612 x

Answer 1

c. y? =+4.198 x

Explanation:

Hello!

Using the given data you need to estimate the equation of linear regression.

Dependent variable:

Y: Annual percentage change in stock price for a company.

Independent variable:

X: Annual percentage change in profits for the company.

The population regression line equation is:

`Y_i= \alpha + \beta X_i + E_i`

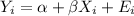
To estimate the equation you need to find the point estimator for α and β.

The following formulas are the ones to use:

α ⇒ a= y[bar] - bX[bar]

β ⇒ b= (∑xy - [(∑x)(∑y)]/n)/(∑X²-(∑x)²/n)

As you can see you need to make several summatories before calculating the values of a and b:

n= 7

∑x= 36.30

∑x²= 667.09

∑y= 51.60

∑y²= 747.98

∑xy= 560.74

Sample mean of de dependent variable Y[bar]= ∑y/n= (51.60/7)= 7.37

Sample mean of the independent variable X[bar]= ∑x/n= (36.30/7)= 5.19

b=
`(560.74-((36.3*51.6))/(7) )/(667.09-((51.60)^2)/(7) )`

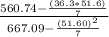
b= 0.6122

a=
`7.37-(0.61*5.19)`

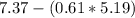
a= 4.196

The estimated regression equation is:

Y= 4.196 + 0.6122x

I hope it helps!