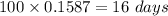Answer:
Explanation:
Given
mean

standard deviation

The no of sample boxes weigh Every morning is 25
Average weight is 1 % more than average
i.e.

The company re-calibrates the machine
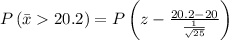
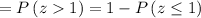

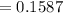
Therefore the Probability that the average weight of box is more than 20.2 ounce is 0.1587
No of days the machine is expected to re-calibrate is