Question

In making plans for an executive traveler’s club, an airline would like to estimate the proportion of its current customers who would qualify for membership. A random sample of 500 customers yielded 40 who would qualify.

(a) Test the hypothesis H0 : p = 0.05 vs Ha : p < 0.05 by constructing reject region at α = 0.1 state what action the airline should take.
(b) Compute the p-value using R.

Answer 1

a)
`\hat p = 0.05 -1.28 \sqrt{(0.05 (1-0.05))/(500)}=0.0375`

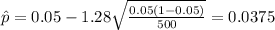
So the rejection zone would be given by
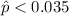`\hat p <0.035` In our case since the estimated proportion is 0.08 we are not on the rejection zone so we FAIL to reject the null hypothesis.

b) prop.test(40, 500, p = 0.05,alternative = c("less"),conf.level = 0.95, correct = FALSE)

With the following output

1-sample proportions test without

continuity correction

data: 40 out of 500, null probability 0.05

X-squared = 9.4737, df = 1, p-value = 0.999

alternative hypothesis: true p is less than 0.05

95 percent confidence interval:

0.000000 0.102291

sample estimates:

p

0.08

Explanation:

Data given and notation

n=500 represent the random sample taken

X=40 represent the customers who would qualify for membership

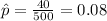`\hat p=(40)/(500)=0.08` estimated proportion of adults that said that it is morally wrong to not report all income on tax returns

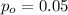`p_o=0.05` is the value that we want to test

`\alpha` represent the significance level

z would represent the statistic (variable of interest)

Alternative hypothesis:
`p < 0.05`

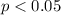
When we conduct a proportion test we need to use the z statisitc, and the is given by:

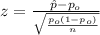`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
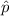`\hat p` is significantly different from a hypothesized value
`p_o`.

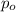Part a

The population proportion have the following distribution

`p \sim N(p,\sqrt{(p(1-p))/(n)})`

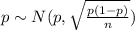
And we know that the z score is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}`

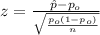
And we are interested to find the value of

`-1.28=\frac{\hat p -0.05}{\sqrt{(0.05 (1-0.05))/(500)}}`

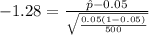
And if we solve for
`hat p[\tex] we got:</p><p>[tex]\hat p = 0.05 -1.28 \sqrt{(0.05 (1-0.05))/(500)}=0.0375`

So the rejection zone would be given by
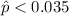`\hat p <0.035` In our case since the estimated proportion is 0.08 we are not on the rejection zone so we FAIL to reject the null hypothesis.

Part b

prop.test(40, 500, p = 0.05,alternative = c("less"),conf.level = 0.95, correct = FALSE)

With the following output

1-sample proportions test without

continuity correction

data: 40 out of 500, null probability 0.05

X-squared = 9.4737, df = 1, p-value = 0.999

alternative hypothesis: true p is less than 0.05

95 percent confidence interval:

0.000000 0.102291

sample estimates:

p

0.08