Answer:
a)
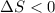
b) entropy of the sistem equal to a), entropy of the universe grater than a).
Step-by-step explanation:
a) The change of entropy for a reversible process:
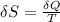
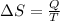
The energy balance:
![\delta U=[tex]\delta Q- \delta W](https://img.qammunity.org/2020/formulas/chemistry/college/sdbt79oppcypfye7o32sl2s6vf14kkhbng.png)
If the process is isothermical the U doesn't change:
![0=[tex]\delta Q- \delta W](https://img.qammunity.org/2020/formulas/chemistry/college/cilbgjqdhunhjdtktws759dq4owz8ywu2h.png)
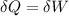
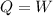
The work:
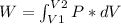
If it is an ideal gas:
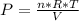
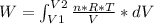
Solving:
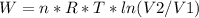
Replacing:
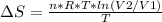
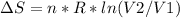
Given that it's a compression: V2<V1 and ln(V2/V1)<0. So:
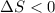
b) The entropy change of the sistem will be equal to the calculated in a), but the change of entropy of the universe will be 0 in a) (reversible process) and in b) has to be positive given that it is an irreversible process.