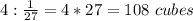Question

A rectangular prism with a volume of 4 cubic units is filled with cubes with side lengths of 1/3 units. How many 1/3 units does it take to fill the prism?

Answer 1

108 cubes

Explanation:

step 1

Find the volume of the cube with side length of 1/3 units

The volume of the cube is equal to

`V=b^3`

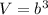
where

b is the side length

we have

`b=(1)/(3)\ units`

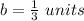
substitute

`V=((1)/(3))^3`

`V=(1)/(27)\ units^3`

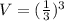
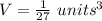
step 2

To find how many cubes are needed to fill the prism, divide 4 cubic units (volume of the rectangular prism) by 1/27 cubic units (volume of one cube)

`4:(1)/(27)=4*27= 108\ cubes`