Question

A ball is thrown eastward into the air from the origin (in the direction of the positive x-axis). The initial velocity is 50 i + 48 k, with speed measured in feet per second. The spin of the ball results in a southward acceleration of 8 ft/s2, so the acceleration vector is a = −8 j − 32 k. Where does the ball land? (Round your answers to one decimal place.) 154.3 ft from the origin at an angle of ° from the eastern direction toward the south.

Answer 1

The ball lands 154.3 ft from the origin at an angle of 13.6° from the eastern direction toward the south.

Step-by-step explanation:

Hi there!

The position vector of the ball is described by the following equation:

r = (x0 + v0x · t + 1/2 · ax · t², y0 + v0y · t + 1/2 · ay · t², z0 + v0z · t + 1/2 · g · t²)

Where:

r = poisition vector of the ball at time t.

x0 = initial horizontal position.

v0x = initial horizontal velocity (eastward).

t = time.

ax = horizontal acceleration (eastward).

y0 = initial horizontal position.

v0y = initial horizontal velocity (southward).

ay = horizontal acceleration (southward)

z0 = initial vertical position.

v0z = initial vertical velocity.

g = acceleration due to gravity.

We have to find at which time the vertical component of the position vector is zero (the ball is on the ground) and then we can calculate the horizontal distance traveled by the ball at that time, using the equations of the horizontal components of the position vector.

Let´s place the origin of the system of reference at the throwing point so that x0 and y0 and z0 = 0.

y = z0 + v0z · t + 1/2 · g · t² (z0 = 0)

0 = 48 ft/s · t - 1/2 · 32 ft/s² · t²

0 = t (48 ft/s - 16 ft / s² · t) (t= 0, the origin point)

0 = 48 ft/s - 16 ft / s² · t

- 48 ft/s / -16 f/s² = t

t = 3.0 s

Now, we can calculate how much distance the ball traveled in that time.

First, let´s calculate the distance traveled in the eastward direction:

x = x0 + v0x · t + 1/2 · ax · t² (x0 = 0, ax = 0 there is no eastward acceleration)

x = 50 ft/s · 3 s

x = 150 ft

And now let´s calculate the distance traveled in southward direction:

y = y0 + v0y · t + 1/2 · ay · t² (y0 = 0 and v0y = 0, initially, the ball does not have a southward velocity).

y = 1/2 · ay · t²

y = 1/2 · (-8 ft/s²) · (3 s)²

y = -36 ft

Then, the final position vector will be:

r = (150 ft, -36 ft, 0)

The traveled distance is the magnitude of the position vector:

`|r| = \sqrt{(150ft)^(2) + (-36ft)^(2)} = 154.3 ft`

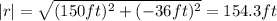
To calculate the angle, we have to use trigonometry (see attached figure):

cos angle = adjacent side / hypotenuse

cos α = x/r

cos α = 150 ft / 154.3 ft

α = 13.6°

The ball lands 154.3 ft from the origin at an angle of 13.5° from the eastern direction toward the south.