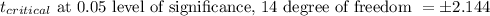Answer:
a)
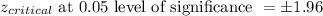
b)
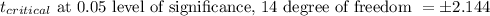
Explanation:
We are given the following information in the question:
Sample size = 15
The population is normally distributed and the mean height of the population is going to be estimated with 95% confidence.
We have to find the appropriate critical value that should be used to build the 95 confidence level.
Confidence interval:

If the population standard deviation is given, we use the z-critical value.
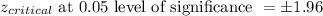
If the population standard deviation is not given, we use the t-critical value.