Answer:
a)
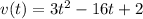
b) The velocity after 3 seconds is -3m/s.
c)
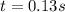 and
and
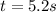 .
.
Explanation:
The position is given by the following equation.
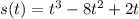
(a) Find the velocity at time t.
The velocity is the derivative of position. So:
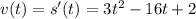 .
.
(b) What is the velocity after 3 seconds?
This is v(3).
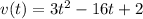

The velocity after 3 seconds is -3m/s.
(c) When is the particle at rest?
This is when
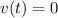 .
.
So:
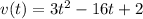
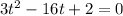
This is when
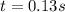 and
and
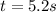 .
.