Question

Your school's talent show a feature 16 solo acts and three ensemble acts. The show will last 141 minutes. The eight solo performers judged best Will give a repeat performance at the second 93 minute show, which will also feature the three ensemble acts. Each solo act lasts x minutes and each ensemble act lasts y minutes.

Answer 1

The system of equation which models the situation are

`\left \{ {{16x+3y =141} \atop {8x+3y=93}} \right.`

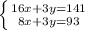
Solo Act lasted for 6 mins and ensemble acts lasted for 15 mins.

Explanation:

Let number of minutes solo act lasted be 'x'

Let the number of minutes ensemble acts lasted be 'y'

Given:

16 solo acts and three ensemble acts show will last 141 minutes.

Now it means:

Total minutes is equal to sum of Number of solo acts multiplied by number of minutes solo act lasted and Number of ensemble acts multiplied by number of minutes ensemble acts lasted.

Framing in equation form we get;

`16x+3y =141 \ \ \ \ equation \ 1`

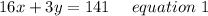
Also Given:

eight solo and three ensemble acts will perform for 93 minutes.

Total minutes is equal to sum of Number of solo acts multiplied by number of minutes solo act lasted and Number of ensemble acts multiplied by number of minutes ensemble acts lasted.

Framing in equation we get;

`8x+3y=93 \ \ \ \ equation\ 2`

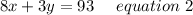
Hence The system of equation which models the situation are

`\left \{ {{16x+3y =141} \atop {8x+3y=93}} \right.`

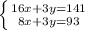
Now Solving the equation to find number of minutes solo and ensemble act lasted we get;

First Subtracting equation 2 from equation 1 we get;

`(16x+3y)-(8x+3y)=141-93\\\\16x+3y-8x-3y= 48\\\\8x=48\\\\x=(48)/(8)=6\ mins`

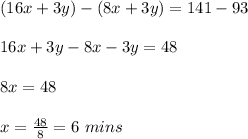
Now solo acts lasted for 6 mins.

Substituting the value of x in equation 1 we get

`16x+3y =141\\\\16*6 +3y =141\\\\96+3y=141\\\\3y = 141-96\\\\3y = 45\\\\y= (45)/(3) = 15\ mins`

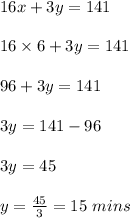
Hence Solo Act lasted for 6 mins and ensemble acts lasted for 15 mins.