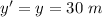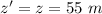Answer:
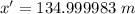
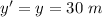
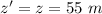
Step-by-step explanation:
Given:
- time,
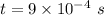
- x coordinates of a particle,
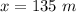
- y coordinates of a particle,
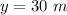
- z coordinates of a particle,
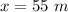
- Relative Speed of frame of reference S' in the +x direction,

- Since the speed of the frame S' is comparable to the speed of light in vacuum therefore the observer from S' frame will observe a contracted length of the dimensions in the direction of motion.
Now from the equation of length contraction:
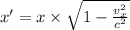
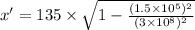
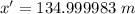
Rest other values will remain unaffected since they are along the axis of motion. So,