Question

Find s15 for the following sequence40,34, 28,22​

Answer 1

- 30

Explanation:

Note the common difference d between consecutive terms in the sequence

d = 34 - 40 = 28 - 34 = 22 - 22 = - 6

This indicates the sequence is arithmetic with sum to n terms calculated as

`S_(n)` =
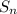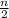`(n)/(2)` [ 2a₁ + (n - 1)d ]

where a₁ is the first term and d the common difference

Here a₁ = 40 and d = - 6, thus

`S_(15)` =
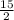`(15)/(2)` [ (2 × 40) + (14 × - 6) ], that is

`S_(15)` = 7.5(80 - 84) = 7.5 × - 4 = - 30

Answer 2

`\displaystyle -44 = s_(15)`

Explanation:

`\displaystyle -6n + 46 = a_n \\ -6[15] + 46 = a_n \\ -90 + 46 = a_n \\ -44 = a_n`

Use the Arithmetic Sequence to figure this out.

I am joyous to assist you anytime.