Question

1. Quadrilateral ABCD has vertices A(-1, 1), B(2, 3), C(6, 0) and D(3, -2). Determine using coordinate geometry whether or not the diagonals* of ABCD a. Bisect each other. B. Are congruent. C. Are perpendicular.1. Quadrilateral ABCD has vertices A(-1, 1), B(2, 3), C(6, 0) and D(3, -2). Determine using coordinate geometry whether or not the diagonals* of ABCD a. Bisect each other. B. Are congruent. C. Are perpendicular.

Answer 1

The Conclusion is

Diagonals AC and BD,

a. Bisect each other

b. Not Congruent

c. Not Perpendicular

Explanation:

Given:

[]ABCD is Quadrilateral having Vertices as

A(-1, 1),

B(2, 3),

C(6, 0) and

D(3, -2).

So the Diagonal are AC and BD

To Check

The diagonals AC and BD

a. Bisect each other. B. Are congruent. C. Are perpendicular.

Solution:

For a. Bisect each other

We will use Mid Point Formula,

If The mid point of diagonals AC and BD are Same Then

Diagonal, Bisect each other,

For mid point of AC

`Mid\ point(AC)=((x_(1)+x_(2) )/(2),(y_(1)+y_(2) )/(2))`

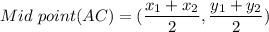
Substituting the coordinates of A and C we get

`Mid\ point(AC)=((-1+6)/(2),(1+0)/(2))=((5)/(2),(1)/(2))`

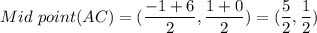
Similarly, For mid point of BD

Substituting the coordinates of B and D we get

`Mid\ point(BD)=((2+3)/(2),(3-2)/(2))=((5)/(2),(1)/(2))`

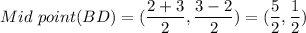
Therefore The Mid point of diagonals AC and BD are Same

Hence Diagonals,

a. Bisect each other

B. Are congruent

For Diagonals to be Congruent We use Distance Formula

For Diagonal AC

`l(AC) = \sqrt{((x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) )}`

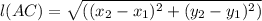
Substituting A and C we get

`l(AC) = \sqrt{((6-(-1))^(2)+(0-1)^(2) )}=√((49+1))=√(50)`

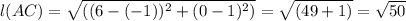
Similarly ,For Diagonal BD

Substituting Band D we get

`l(BD) = \sqrt{((3-2))^(2)+(-2-3)^(2) )}=√((1+25))=√(26)`

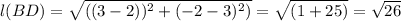
Therefore Diagonals Not Congruent

For C. Are perpendicular.

For Diagonals to be perpendicular we need to have the Product of slopes must be - 1

For Slope we have

`Slope(AC)=(y_(2)-y_(1) )/(x_(2)-x_(1) )`

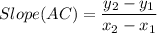
Substituting A and C we get

`Slope(AC)=(0-1)/(6--1)\\\\Slope(AC)=(-1)/(7)`

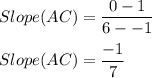
Similarly, for BD we have

`Slope(BD)=(-2-3)/(3-2)\\\\Slope(BD)=(-5)/(1)`

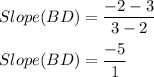
The Product of slope is not -1

Hence Diagonals are Not Perpendicular.