Question

For Christmas, each member of a class

sends the other classmates a card. If
992 cards are exchanged, find the
number of pupils in the class.

Answer 1

There are 32 pupils in the class

Explanation:

Let's say there are N pupils in the class. Then each pupil must send N-1 cards - because it would make no sense to send one to themselves! So each of the N pupils send N-1 cards, which becomes 992 cards in total. In equation form, this is

`N(N-1)=992\\N^2-N-992=0`

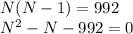
This is a second degree polynomial, which has the solutions

`N=(-b\pm √(b^2-4\cdot a \cdot c))/(2a)`

where
`a=1, b=-1, \text{and }c=-992`

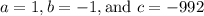
If we insert these numbers in the equation,

`N=(-(-1)\pm √(1^2-4*1*(-992)))/(2*1)\\ = (1\pm √(1+4*992))/(2)\\= (1 \pm 63)/(2)`

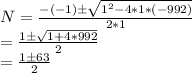
If we choose the solution with the minus sign, we get

N=-31

but this makes no sense! There can't be a negative number of pupils in the class!

So we choose the solution with the plus sign,

`N=(1+63)/(2)\\ =(64)/(2)\\ =32`

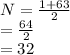
So there are 32 pupils in the class

Answer 2

number of pupils in the class = 32

Explanation:

Let n be the number of students. So n-1 cards will be sent by each student.

n(n-1) =192

n² - n =192

n² - n - 192 = 0

n² - 32n + 31n - (31*32) = 0

n(n - 32) + 31 (n-32) = 0

(n-32)(n+31) = 0

n - 32 = 0 or n + 31 = 0

n = 32 or n = -31 is not possible because no. of students cannot be negative

n= 32