Question

The square of a number decreased by 3 times the number 28 find all possible values for the number

Answer 1

Question:

The square of a number decreased by 3 times the number is 28 find all possible values for the number

Answer:

The possible values of number are 7 and -4

Solution:

Given that the square of a number decreased by 3 times the number is 28

To find: all possible values of number

Let "a" be the unknown number

From given information,

square of a number decreased by 3 times the number = 28

`a^2 - 3a = 28`

`a^2 - 3a - 28 = 0`

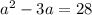
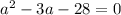
Let us solve the above quadratic equation

`\text {For a quadratic equation } a x^(2)+b x+c=0, \text { where } a \\eq 0`

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

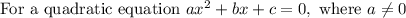
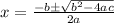
Using the above formula,

`\text { For } a^(2)-3 a-28=0 \text { we have } a=1, b=-3, c=-28`

`\begin{aligned}&a=\frac{-(-3) \pm \sqrt{(-3)^(2)-4(1)(-28)}}{2 * 1}\\\\&a=(3 \pm √(9+112))/(2)\\\\&a=(3 \pm √(121))/(2)=(3 \pm 11)/(2)\\\\&a=(3+11)/(2) \text { or } a=(3-11)/(2)\\\\&a=7 \text { or } a=-4\end{aligned}`

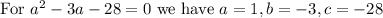
Thus the possible values of number are 7 and -4