Answer:
h = 500 meters; angle = 45°
Step-by-step explanation:
Don't worry the answers are very simple. As we can see in problem 31 we have a right triangle, the right triangle always has a 90° angle. Let's also remember that all the sum of the three angles of a triangle will be equal to 180°.
Using the trigonometric function of cosinus we can find the value for h.
![cos(60)=(h)/(1000) \\h= cos(60)*1000\\h= 500[m]](https://img.qammunity.org/2020/formulas/physics/middle-school/tpovfy8grusy4vdgfk8njpypev8ytjgo9v.png)
Cosinus (angle) = adjacent side / hypotenuse
Hypotenuse = longest side of the right triangle
adjacent side = side of the triangle, near to the angle that we want to find its dimension.
In problem 32 we will use also the trigonometric function. In this case we don't know the hypotenuse dimension therefore the best trigonometric fuction is "tangent"
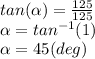
tan (angle) = opposite side / adjacent side