Question

I need help on both a and b of question 1

Answer 1

(a) -0.00017 M/s;

(b) 0.00034 M/s

Step-by-step explanation:

(a) Rate of a reaction is defined as change in molarity in a unit time, that is:

`r = (\Delta c)/(\Delta t)`

Given the following reaction:

`2 N_2O_5 (g)\rightleftharpoons 4 NO_2 (g) + O_2 (g)`

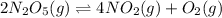
We may write the rate expression in terms of reactants firstly. Since reactants are decreasing in molarity, we're adding a negative sign. Similarly, if we wish to look at the overall reaction rate, we need to divide by stoichiometric coefficients:

`r = -(\Delta [N_2O_5])/(2 \Delta t)`

Reaction rate is also equal to the rate of formation of products divided by their coefficients:

`r = (\Delta [NO_2])/(4 \Delta t) = (\Delta [O_2])/(\Delta t)`

Let's find the rate of disappearance of the reactant firstly. This would be found dividing the change in molarity by the change in time:

`r_(N_2O_5) = (0.066 M - 0.100 M)/(200.00 s - 0.00 s) = -0.00017 M/s`

(b) Using the relationship derived previously, we know that:

`-(\Delta [N_2O_5])/(2 \Delta t) = (\Delta [NO_2])/(4 \Delta t)`

Rate of appearance of nitrogen dioxide is given by:

`r_(NO_2) = (\Delta [NO_2])/(\Delta t)`

Which is obtained from the equation:

`-(\Delta [N_2O_5])/(2 \Delta t) = (\Delta [NO_2])/(4 \Delta t)`

If we multiply both sides by 4, that is:

`-(4 \Delta [N_2O_5])/(2 \Delta t) = (\Delta [NO_2])/(\Delta t)`

This yields:

[tex]r_{NO_2} = \frac{\Delta [NO_2]}{\Delta t} = -2\frac{\Delta [N_2O_5]}{ \Delta t} = -2\cdot (-0.00017 M/s) = 0.00034 M/s[tex]