Question

Find the equation of the line that cuts through (0,5) and (1,2)?

Answer 1

The equation of the line that cuts through (0,5) and (1,2) is y = -3x + 5

Solution:

Given that we have to find equation of the line that cuts through (0,5) and (1,2)

The equation of line passing through points
`(x_1, y_1)` and
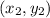`(x_2, y_2)` is given as:

`y - y_1 = m(x - x_1)`

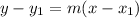
Where "m" is the slope of line

Let us first find slope of line

The slope of line is given as:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text{ Substituting }  (x_1, y_1) = (0, 5) \text{ and } (x_2, y_2) = (1, 2)`

`m=(2-5)/(1-0)=-3`

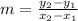
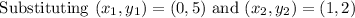
Thus the required equation of line is:

`y - 5 = -3(x - 0)\\\\y - 5 = -3x\\\\y = -3x + 5`

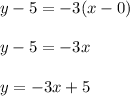
Thus the equation of line is found