Question

F(t) = -(t - 2)(t – 15)

1) What are the zeros of the function?
Write the smaller t first, and the larger t second.

Answer 1

Smaller t = 2

Larger t = 5

Explanation:

Given:

The given function is.

`f(t)=-(t-2)(t-5)`

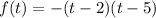
Find the zeros of the function.

Solution:

`f(t)=-(t-2)(t-5)`

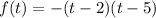
Simplify the equation above equation.

`f(t)=-(t^(2)-5t-2t+10)`

`f(t)=-(t^(2)-7t+10)`

`f(t)=-t^(2)+7t-10`

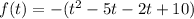
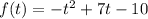
Now, we first find the root of the above equation.

Use quadratic formula with
`a=-1, b=7, c=-10`.

`t=\frac{-b\pm \sqrt{(b)^(2)-4ac}}{2a}`

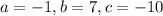Put a, b and c value in above equation.

`t=\frac{-7\pm \sqrt{(7)^(2)-4(-1)(-10)}}{2(-1)}`

`t=(-7\pm √(49-4* 10))/(-2)`

`t=(-7\pm √(49-40))/(-2)`

`t=(-7\pm √(9))/(-2)`

`t=(-7\pm 3)/(-2)`

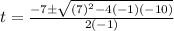
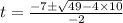
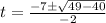
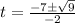
For positive sign

`t=(-7 + 3)/(-2)`

`t=(-4)/(-2)`

t = 2

For negative sign

`t=(-7 - 3)/(-2)`

`t=(-10)/(-2)`

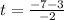
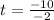
t = 5

Put t = 2 in given function.

`f(t)=-(2-2)(2-5)=0`

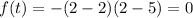
Put t = 5 in given function.

`f(t)=-(5-2)(5-5)=0`

So, the zeros of the function is t = 2 or 5

Therefore, the smaller value of t = 2 and larger value of t = 5.