Question

The radius,r, of a sphere is increasing at a constant rate of 0.05 meters per second.

A. At the time when the radius of the sphere is 12 meters, what is ther rate of increase in its volume?
B. At the time when the volume of the sphere is 36pi cubic meters, what is the rate of increase in its surface area?
C. Express the rate at which the volume of the sphere changes with respect to the surface are of the sphere (as a function of r)
Please include steps. Thanks so much!

Answer 1

Question:

C. Express the rate at which the volume of the sphere changes with respect to the surface are of the sphere (as a function of r)

Explanation:

Here's how you solve part C of this question.

Start with what you know:

dV/dt = 4pir^2 x (dr/dt)

(dr/dt) = 0.05

S(r) = (Surface Area) = 4pir^2

So, since S(r) is equal to 4pir^2, we replace 4pir^2 with S(r). We also know that (dr/dt) = 0.05, so we replace (dr/dt) with 0.05.

Now the equation should look like this:

dV/dt = 0.05 x S(r) <----- (your answer).

Hope this helped!! :)

Answer 2

A. 90.5 cubic meters pet second.

B. 3.77 square meters per second.

C.
`(dV)/(dS) = (r)/(2)`

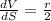
Explanation:

The radius of a sphere is increasing at a constant rate of 0.05 meters per second.

Therefore,
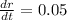`(dr)/(dt) = 0.05` ......... (1)

A. Now, volume of the sphere is given by

`V = (4)/(3)\pi  r^(3)`

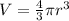
Now, differentiating both sides with respect to t we get,

`(dV)/(dt) = (4)/(3)\pi (3r^(2)) (dr)/(dt) = 4\pi r^(2) (dr)/(dt)`

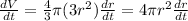
Then at r = 12 meters, the rate of increase in volume will be

`(dV)/(dt) = 4 * ((22)/(7)) * 12^(2) * 0.05 = 90.5` cubic meters pet second. {From equation (1)}

B. When the volume of the sphere is 36π cubic meters, then

`(4)/(3)\pi r^(3) = 36\pi`

⇒
`r^(3) = 27`

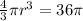
⇒ r = 3 meters.

Now, surface area of a sphere is given by

S = 4πr² .......... (2)

Differentiating both sides with respect to time (t) we get,

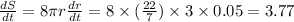`(dS)/(dt) = 8\pi r(dr)/(dt) = 8 * ((22)/(7)) * 3 * 0.05 = 3.77` square meters per second. {From equation (1)}

C. Now,
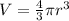`V = (4)/(3)\pi  r^(3)` and S = 4πr²

⇒
`V = (1)/(3) (4\pi r^(2))r = (Sr)/(3)`

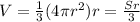
Now, differentiating with respect to S both sides we get,

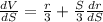`(dV)/(dS) = (r)/(3) + (S)/(3) (dr)/(dS)` ......... (3)

Now, we have, S = 4πr²

Differentiating with respect to S both sides, we get

`1 = 8\pi r(dr)/(dS)`

⇒
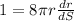
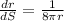`(dr)/(dS) = (1)/(8\pi r )` ......... (4)

Now, from equations (2), (3) and (4) we get,

`(dV)/(dS) = (r)/(3) + (4\pi r^(2) )/(3) * (1)/(8\pi r )`

⇒
`(dV)/(dS) = (r)/(3) + (r)/(6)`

⇒
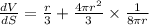
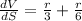
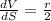`(dV)/(dS) = (r)/(2)` (Answer)