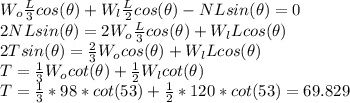Question

"Q 12.10: A 98 N object is placed 1/3 of the way up a 120 N ladder, which makes an angle of 53 degrees with the horizontal. The lower end is also fastened to the wall by a rope, and both the wall and floor are frictionless. What is the tension in the rope?"

Answer 1

68.829 N

Step-by-step explanation:

The given parameters are:

Weight of ladder,
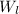`W_l` = 120 N

Weight of object,
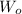`W_o` = 98 N

Angle,
`\theta` = 53°

And we also know that, while

Length of ladder = L

Distance the object is placed = L/3

If we apply translational equilibrium horizontally, then
`T-N=0`, so
`T = N`

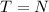
If we apply rotational equilibrium about the distance the object is placed, then

`W_o(L)/(3)cos(\theta) + W_l(L)/(2)cos(\theta) - NLsin(\theta) = 0\\2NLsin(\theta) = 2W_o(L)/(3)cos(\theta)+W_lLcos(\theta)\\2Tsin(\theta) = (2)/(3)W_ocos(\theta)+W_lLcos(\theta)\\T = (1)/(3)W_ocot(\theta) + (1)/(2)W_lcot(\theta)\\T = (1)/(3) * 98 * cot(53) + (1)/(2) * 120 * cot(53) = 69.829`