Question

One of the hazards of nuclear explosions is the generation of 90Sr andits subsequent incorporation in place of calcium in bones. This nuclide emitsβrays of energy 0.55 MeV, and has a half-life of 28.1 y. Suppose 1.00 μg wasabsorbed by a newly born child. How much will remain after (a) 18 y, (b) 70 yif none is lost metabolically?

Answer 1

Step-by-step explanation:

Initial mass of the isotope 90-Sr in baby= 1.00 μg

Formula used :

`N=N_o* e^(-\lambda t)\\\\\lambda =\frac{0.693}{t_{(1)/(2)}}`

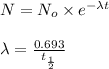
where,

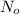`N_o` = initial mass of isotope

N = mass of the parent isotope left after the time, (t)

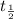`t_{(1)/(2)}` = half life of the isotope = 28.1 years

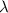`\lambda` = rate constant

`N=N_o* e^{-((0.693)/(t_(1/2)))* t}`

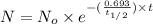
a) Time taken by the sample, t = 18 years

`N=1.00 \mu g* e^{-(0.693)/(28.1 years)* 18 years}`

`N = 0.6415 \mu g`

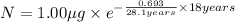
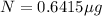
0.6415 μg will remain after 18 years.

b) Time taken by the sample, t = 70 years

`N=1.00 \mu g* e^{-(0.693)/(28.1 years)* 70 years}`

`N = 0.1779\mu g`

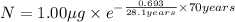
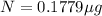
0.1779 μg will remain after 70 years.