Question

A machine starts dumping sand at the rate 20 m^3/min, forming a pile in the shape of a cone. The height of the pile is always twice the length of the base diameter. After 5 minutes, how fast is the base radius increasing? Please include steps. Thanks!

Answer 1

Base radius is increasing by 2.88 m after 5 minutes

Explanation:

Given:-

Height of cone (h) =2
`*` base diameter(d)

`h=2* d`

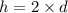
Machine starts dumping sand at the rate of 20
`m^(3)/min`

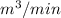
So,

Volume of cone in 1 min = 20
`m^(3)`

Now, Volume of cone in 5 mins = Volume of cone in 1 min
`* 5`

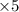
Volume of cone in 5 mins = 20
`* 5`

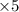
Volume of cone in 5 mins = 100
`m^(3)` ---------(equation 1)

Now, Let base diameter of cone = b

height of the cone = h

formula for volume of cone is,

Volume of cone (V) =
`\pi* r^(2) *(h)/(3)`

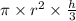
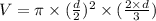`V=\pi*( (d)/(2) )^(2)*((2* d)/(3))` ----(since r=
`(d)/(2)`)

`V=\pi*(d^(2) )/(4) * (2d)/(3)`

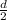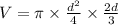
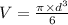`V=(\pi* d^(3) )/(6)` ---------(equation 2)

Now substituting equation 1 in equation 2,

`100=(\pi* d^(3) )/(6)`

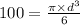
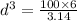`d^(3)=(100* 6)/(3.14)` ---------(as
`\pi=3.14`)

`d^(3) =(600)/(3.14)`

`d^(3) =191.08`

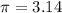By cube rooting both the sides we get,

`\sqrt[3]{d} =\sqrt[3]{191.08}`

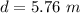`d=5.76 \ m` ----------------(diameter)

`as\ r=(d)/(2)`

`r=(5.76)/(2)`

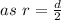
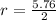
`r=2.88\ m` ---------------(radius of base at 5 mins)

Therefore base radius is increasing by 2.88 m after 5 minutes