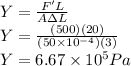Answer:
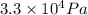
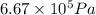
Step-by-step explanation:
Complete statement of the question is
A relaxed biceps muscle requires a force of 25.0 N for an elongation of 3.0 cm; the same muscle under maximum tension requires a force of 500 N for the same elongation. Find Young's modulus (Pa) for the muscle tissue under each of these conditions .The muscle is assumed to be a uniform cylinder with length 0.200 m and cross-sectional area 50.0 cm^2.
For relaxed muscle :
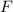 = force required = 25 N
= force required = 25 N
 = Normal length = 0.2 m = 20 cm
= Normal length = 0.2 m = 20 cm
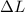 = elongation in length = 3 cm
= elongation in length = 3 cm
 = Area of cross-section = 50 cm² = 50 x 10⁻⁴ m²
= Area of cross-section = 50 cm² = 50 x 10⁻⁴ m²
 = Young's modulus for the muscle
= Young's modulus for the muscle
Young's modulus is given as

Under maximum tension :
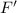 = force required = 500 N
= force required = 500 N
 = Normal length = 0.2 m = 20 cm
= Normal length = 0.2 m = 20 cm
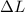 = elongation in length = 3 cm
= elongation in length = 3 cm
 = Area of cross-section = 50 cm² = 50 x 10⁻⁴ m²
= Area of cross-section = 50 cm² = 50 x 10⁻⁴ m²
 = Young's modulus for the muscle
= Young's modulus for the muscle
Young's modulus is given as