Question

Write the following expression in radical form: x^3/2​

Answer 1

`x√(x)`

Explanation:

Given:

The given expression is.

`x^{(3)/(2)}`

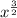
Now, we need to write the given expression in radical form.

Solution:

First, we can rewrite the term as:

`x^{3* (1)/(2)`

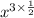
Now, we can use this rule of exponents to rewrite the term again:

`x^(a* b) = (x^(a))^(b)`

`x^{3* (1)/(2)} = (x^(3))^{(1)/(2)}`

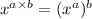
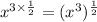
Now, we can use this rule to write the term as an radical:

`x^{(1)/(n)} = \sqrt[n]{x}`

`(x^(3))^{(1)/(2)} = \sqrt[2]{x^(3)}`

`(x^(3))^{(1)/(2)} = x√(x)`

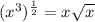
Therefore, the redical form of the given expression is
`x√(x)`