Question

Hanging from a horizontal beam are nine simple pendulums of the following lengths: (a) 0.080, (b) 0.26, (c) 0.49, (d) 0.90, (e) 2.6, (f) 3.3, (g) 3.8, (h) 5.4, and (i) 6.3 m. Suppose the beam undergoes horizontal oscillations with angular frequencies in the range from 2.00 rad/s to 4.00 rad/s. Which of the pendulums will be (strongly) set in motion?

Answer 1

Step-by-step explanation:

This is the case of forced oscillation . The pendulum having the same or matching time period or angular frequency with that of angular frequency of external periodic force , will be in resonance having largest amplitude.

Angular frequency of pendulum having length .9 m

=
`\sqrt{(g)/(l ) }`

l = .9

angular frequency

=
`\sqrt{(10)/(0.9 ) }`

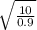
= 3.33 rad / s

If we calculate angular frequencies of pendulum of all lengths given , we will find that other lengths do not give angular frequency falling between 2 and 4 radian . So only pendulum having length of .9 m will have vibration of maximum amplitude.