Question

A stock has a price of 100. It is expected to pay a dividend of $2 per share at year-end. An at-the-money European put option with 1 year maturity sells for $7. If the annual interest rate is 5%, what must be the price of an at-the-money European call option on the stock with 1 year maturity.

Answer 1

$9.86

Step-by-step explanation:

Suppose there was no dividend, we can use the put-call formula

`C + X / (1+r)^t = S + P`

Making C subject of the formula,

`C = S + P - X / (1+r)^t`

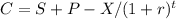
where

C = call premium

P = put premium

X = strike price

r = annual interest rate

t = time (in years)

S = initial price of underlying

and get

C = 100 + 7 - 100 / 1.05

C = 107 - 95.24 = 11.76

Since there was a dividend of $2 power share at year-end, so the stock price will be 100 + 2 = 102.

Hence, we have the formula

C = 100 + 7 - 102 / 1.05

C = 107 - 97.14 = 9.86

$9.86 must be the price of a 1-year at-the-money European call option of the stock.